カーブ上の点
| AutoLISP関数 |
|---|
| (vlax-curve-getStartPoint curve-obj) |
| curve-obj:【図形名】、またはVLAオブジェクト |
| カーブの始点(WCS)を返します。 |
| 戻り値:リスト |
| AutoLISP関数 |
|---|
| (vlax-curve-getEndPoint curve-obj) |
| curve-obj:【図形名】、またはVLAオブジェクト |
| カーブの終点(WCS)を返します。 |
| 戻り値:リスト |
vlax-curve-getStartPoint 関数は、カーブの始点を返します。
vlax-curve-getEndPoint 関数は、カーブの終点を返します。
座標系はWCSに拠ります。
curve-obj 引数には、調べたいカーブの【図形名】か VLA オブジェクトを指定します。
戻り値は、該当の座標(WCS)を表すリストが返ります。放射線または構築線の無限遠点は nil となります。閉じた図形は、始点と終点が同値になります。
下は、図形を選択すると、図形タイプと、始点と終点の座標を表示します。
(while (setq ename (car (entsel "\n図形を選択(選択なしで終了)[最後(L)]:"))) (setq edata (entget ename)) (prompt "\n") (prompt (cdr (assoc 0 edata))) (prompt " : 始点 ") (prompt (vl-princ-to-string (vlax-curve-getStartPoint ename))) (prompt " 終点") (prompt (vl-princ-to-string (vlax-curve-getEndPoint ename))) )
実行すると、例えば以下のように表示されます。
図形を選択(選択なしで終了)[最後(L)]:
LINE : 始点 (61.1887 83.5275 0.0) 終点(346.812 83.5275 0.0)
図形を選択(選択なしで終了)[最後(L)]:
LWPOLYLINE : 始点 (58.1663 160.553 0.0) 終点(58.1663 160.553 0.0)
図形を選択(選択なしで終了)[最後(L)]:
POLYLINE : 始点 (233.092 197.555 0.0) 終点(233.092 197.555 0.0)
図形を選択(選択なしで終了)[最後(L)]:
SPLINE : 始点 (197.861 289.553 0.0) 終点(197.861 289.553 4.0208e-014)
図形を選択(選択なしで終了)[最後(L)]:
CIRCLE : 始点 (510.364 89.9182 0.0) 終点(510.364 89.9182 0.0)
| AutoLISP関数 |
|---|
| (vlax-curve-getPointAtParam curve-obj param) |
| curve-obj:【図形名】、またはVLAオブジェクト param:実数 |
| 指定されたパラメータの値でのカーブ上の点 (WCS) を返します。 |
| 戻り値:リスト |
vlax-curve-getPointAtParam関数は、指定した【パラメータ】のカーブ上の点の座標を返します。
curve-obj 引数には、調べたいカーブの【図形名】か VLA オブジェクトを指定します。
param 引数は、得たい点の【パラメータ】を実数で指定します。
戻り値は、カーブ上の点の座標 (WCS) を格納したリストが返ります。周期的な【パラメータ】を受け付けるカーブの場合を除いて【パラメータ】の値の範囲が不正だった場合は nil となります。
注意点として、曲線の 2D/3D ポリラインの場合は直線で近似した形の座標を返します。つまり、細かく座標をサンプリングしても滑らかな曲線にはならず角があります。画面表示上は問題にはなりませんが幾何計算上は認識しておく必要があります。
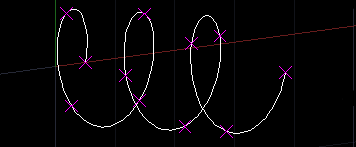
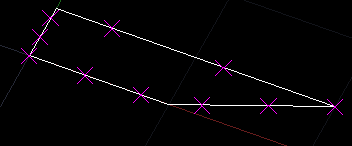
次の例は、図形を選択すると、【パラメータ】の範囲を10等分した点の座標を画面に表示するものです。表示したクロス状のマーカーは、REDRAW コマンドや画面を移動すると消えます。
(setq *clossData* ;_ DCS
'(6 (-0.5 -0.5 0.0) (0.5 0.5 0.0) 6 (-0.5 0.5 0.0) (0.5 -0.5 0.0))
)
(defun grvecs:TransformMatrix (origin size / point scale) ;_ origin(UCS)
(setq point (trans origin acUcs acDisplayDCS)
scale (* size (/ (getvar "VIEWSIZE") (cadr (getvar "SCREENSIZE"))))
)
(list (list scale 0.0 0.0 (car point))
(list 0.0 scale 0.0 (cadr point))
(list 0.0 0.0 scale (caddr point))
'(0.0 0.0 0.0 1.0)
)
)
(defun drawCloss (point /) ;_ point(UCS)
(grvecs *clossData* (grvecs:TransformMatrix point 10.0))
)
(defun ParamList:sub (index)
(if (<= index n)
(cons (+ start (* step index)) (ParamList:sub (1+ index)))
)
)
(defun ParamList (start end n / step)
(setq step (/ (float (- end start)) n))
(ParamList:sub 0)
)
(while
(setq ename (car (entsel "\n図形を選択(選択なしで終了)[最後(L)]:")))
(setq startParam (vlax-curve-getStartParam ename)
endParam (vlax-curve-getEndParam ename)
)
(if (and startParam endParam)
(foreach param (ParamList startParam endParam 10.0)
(drawCloss
(trans (vlax-curve-getPointAtParam ename param) acWorld acUCS)
)
)
)
)
実行例は、以下のような画面です。【パラメータ】は幾何学上必ずしも等間隔というわけではないことが分かります。
| AutoLISP関数 |
|---|
| (vlax-curve-getPointAtDist curve-obj dist) |
| curve-obj:【図形名】、またはVLAオブジェクト dist:実数 |
| 指定された始点からの距離にあるカーブ上の点 (WCS) を返します。 |
| 戻り値:リスト |
vlax-curve-getPointAtDist 関数は、指定した始点からの距離でカーブ上の点の座標を得ます。
curve-obj 引数には、調べたいカーブの【図形名】か VLA オブジェクトを指定します。
dist 引数には、始点からの距離を指定します。
戻り値は、カーブ上の点の座標 (WCS) を格納したリストが返ります。距離の値が不正だった場合は nil が返ります。
注意点として、曲線の 2D/3D ポリラインの場合は直線で近似した形の座標を返します。つまり、細かく座標をサンプリングしても滑らかな曲線にはならず角があります。画面表示上は問題にはなりませんが幾何計算上は認識しておく必要があります。さらに、ポリラインで終点の距離を指定して終点の座標を得ようとすると nil となりますので、座標を正しく得られたか確認が必要です。終点に十分近ければ、直接終点の座標を得るように、次のように関数をラップして使う方が使い勝手が良いでしょう。
(defun curve:point:dist (ename dist / clength)
(setq clength (vlax-curve-getDistAtParam
ename
(vlax-curve-getEndParam ename)
)
)
(if (equal dist clength (* clength (expt 10.0 -10)))
(vlax-curve-getEndPoint ename)
(vlax-curve-getPointAtDist ename dist)
)
)
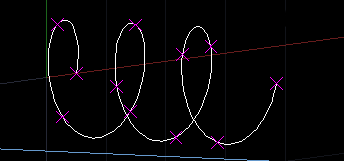
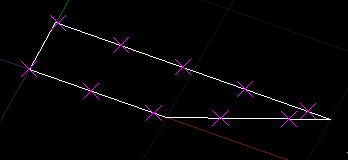
次の例は、図形を選択すると、カーブの長さを10等分した点の座標を表示するものです。上のラップした関数も使います。表示したクロス状のマーカーは、REDRAWコマンドや画面を移動すると消えます。
(setq *clossData* ;_ DCS
'(6 (-0.5 -0.5 0.0) (0.5 0.5 0.0) 6 (-0.5 0.5 0.0) (0.5 -0.5 0.0))
)
(defun grvecs:TransformMatrix (origin size / point scale) ;_ origin(UCS)
(setq point (trans origin acUcs acDisplayDCS)
scale (* size (/ (getvar "VIEWSIZE") (cadr (getvar "SCREENSIZE"))))
)
(list (list scale 0.0 0.0 (car point))
(list 0.0 scale 0.0 (cadr point))
(list 0.0 0.0 scale (caddr point))
'(0.0 0.0 0.0 1.0)
)
)
(defun drawCloss (point /) ;_ point(UCS)
(grvecs *clossData* (grvecs:TransformMatrix point 10.0))
)
(defun ParamList:sub (index)
(if (<= index n)
(cons (+ start (* step index)) (ParamList:sub (1+ index)))
)
)
(defun ParamList (start end n / step)
(setq step (/ (float (- end start)) n))
(ParamList:sub 0)
)
(while
(setq ename (car (entsel "\n図形を選択(選択なしで終了)[最後(L)]:")))
(setq endParam (vlax-curve-getEndParam ename))
(if endParam
(foreach dist (ParamList 0.0
(vlax-curve-getDistAtParam ename endParam)
10.0
)
(drawCloss
(trans (curve:point:dist ename dist) acWorld acUCS)
)
)
)
)
実行例は、以下のような画面です。距離で等間隔に割り当てたので、等間隔にマーカーが表示されます。
| AutoLISP関数 |
|---|
| (vlax-curve-getClosestPointTo curve-obj givenPnt [extend]) |
| curve-obj:【図形名】、またはVLAオブジェクト givenPnt:リスト extend:nil、またはnil以外 |
| 与えられた点(WCS)にもっとも近接するカーブ上の点(WCS)を返します。 |
| 戻り値:リスト |
| AutoLISP関数 |
|---|
| (vlax-curve-getClosestPointToProjection curve-obj givenPnt normal [extend]) |
| カーブと与えられた点(WCS)を任意の平面に投影した場合に最も近接する点を求め、それに対応する元のカーブ上の点(WCS)を返します。 |
| 指定された始点からの距離にあるカーブ上の点 (WCS) を返します。 |
| 戻り値:リスト |
vlax-curve-getClosestPointTo 関数と vlax-curve-getClosestPointToProjection 関数は、与えられた座標からのカーブ上の近接点を返します。近接点の求め方が、vlax-curve-getClosestPointTo 関数の場合は三次元上の距離で測られます。vlax-curve-getClosestPointToProjection 関数の場合は、任意の平面に投影したカーブと点の距離で測られます。
curve-obj 引数には、調べたいカーブの【図形名】か VLA オブジェクトを指定します。
givenPnt 引数には、調べる点(WCS)を与えます。
extend 引数は、nil 以外の時にはカーブを延長して調べます。延長のされ方は、直線や円弧といった延長の仕方が自明なものに限られるようです。ポリラインやスプラインでは延長の効果は見られません。
vlax-curve-getClosestPointToProjection 関数の投影される平面は、normal 引数により平面の法線( Z 軸の方向)を表すベクトルをリストで指定します。
下は二つの関数の近接点の求め方の違いを表したものです。どちらもシアンの直線上の点からグリーンのらせんへの近接点をとって、二つの点の間をマジェンタの直線で結んでいます。vlax-curve-getClosestPointToProjection 関数の場合は、normal 引数に (0.0 1.0 0.0) を指定して、ZX 平面に投影した近接点を取っています。

ZX 平面から見たモデルは下のようになります。vlax-curve-getClosestPointToProjection 関数が ZX 平面に投影を行ってから近接点を求めているという動作が判ります。
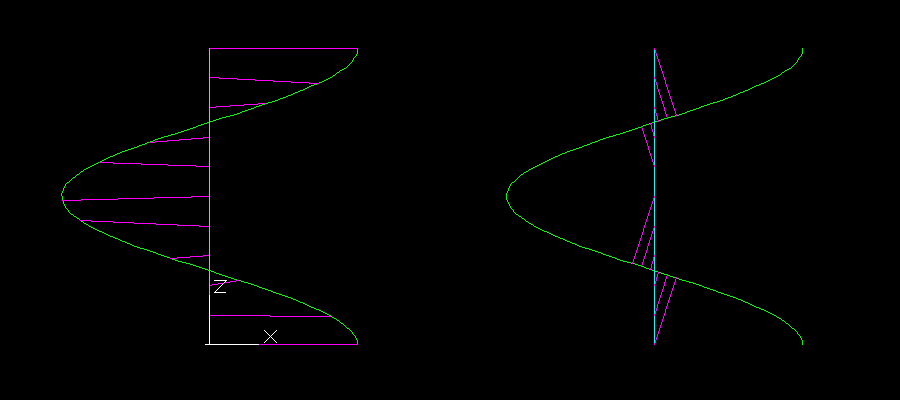
一方で vlax-curve-getClosestPointTo 関数のマジェンタの線が正投影で完全な水平の平行線にはなっていないので、これらの近接点を求める関数の結果には誤差があることも認識しておいた方が良いでしょう。この誤差は人間の目からみると明らかに向こうの点に飛んでしまうこともあります。精度は信用できません。