変換マトリックス

自在に図形の座標を移動・回転・拡大するには変換マトリックスと呼ばれる行列を使います。AutoLISP の関数の中にはこの変換マトリックスを用いるものもあります。ここでは線形代数の行列の知識が必要です。

変換マトリックスは、ある座標を移動・回転・拡大する 4 × 4 の正方行列です。適切に変換マトリックスを設定すれば、ある座標系から別の座標系に座標を変換することができます。そして、変換マトリックスは独自の座標系そのものを表すと解釈することもできます。

下は、最も基本的な変換マトリックスで、変換しても変わらないものです。すなわち、変換マトリックスの単位行列 E です。

行列の計算を展開してみれば明らかです。変換する XYZ 座標につづく 1 は行列計算の都合上付加されたものです。

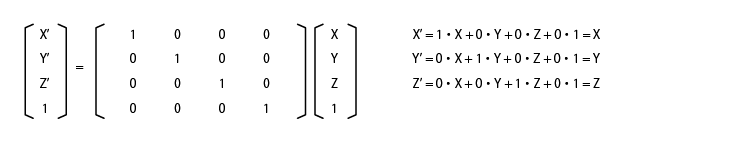
座標を (Tx,Ty,Tz) だけ平行移動するマトリックスは次のようになります。

行列の計算を展開すると以下のようになります。

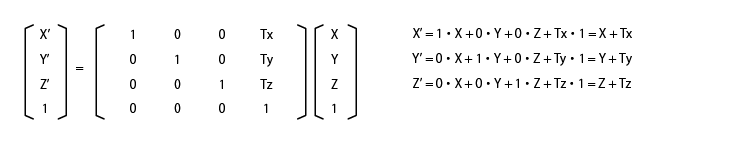
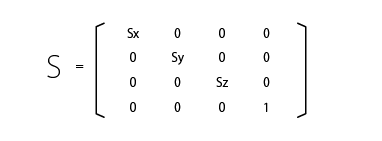
原点を基準に、XYZ 方向にそれぞれ (Sx,Sy,Sz) 倍に座標をスケールする変換マトリックスは次のようになります。原点 (0.0 0.0 0.0) がスケールする基準であることに注意してください。

行列の計算を展開すると以下のようになります。

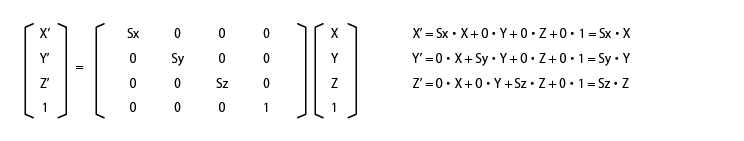
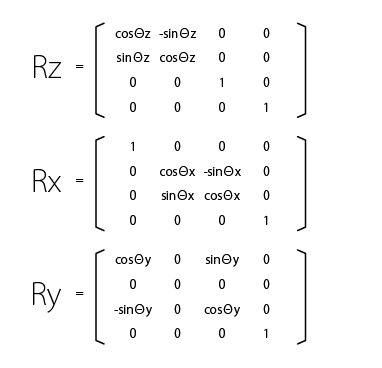
最後に回転に関する変換マトリックスは、X 軸 Y 軸 Z 軸に関するものの三種類あります。スケール変換と同じく原点 (0.0 0.0 0.0) を通る座標軸が回転の基準であることに注意してください。三角関数が出てくるので具体的な計算は直感的では無くなりますが、いずれも行列という形で表されるのが線形代数の便利なところです。

回転の向きは、各軸とも右ねじの法則によります。すなわち、値が大きくなる方向に向かって右回りが回転の正の方向です。

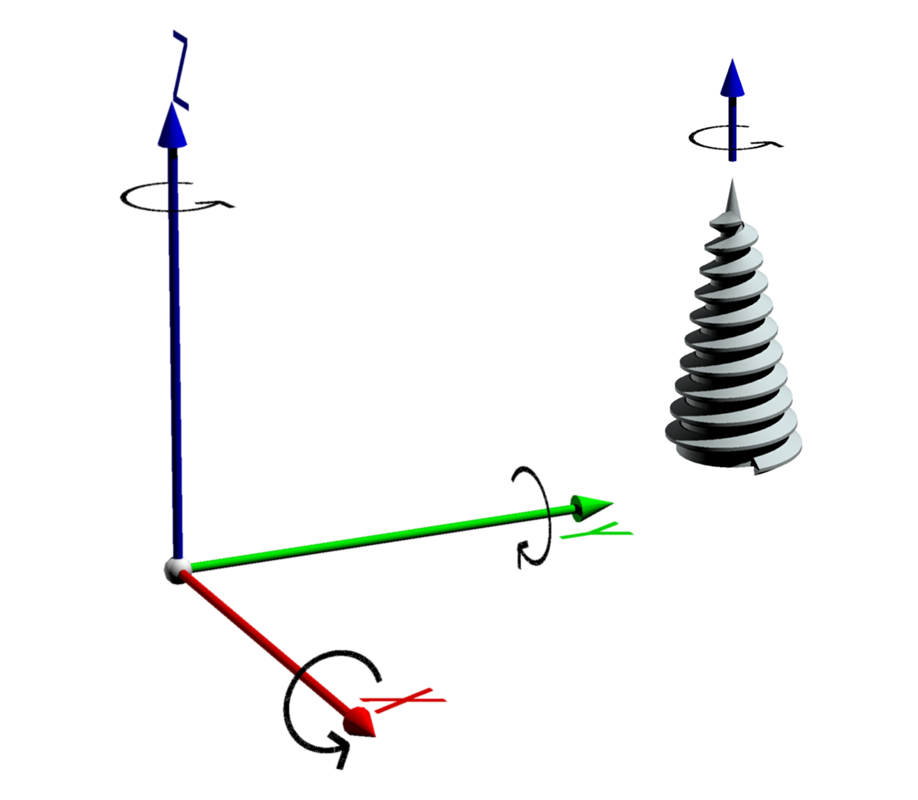
回転の変換は X→Y→Z 軸と順を追って行うのが一般的です。回転する軸の順番を変えると結果は異なります。複数合わせると混乱しやすいので、そのイメージを確認します。

	パース	上から見た図
0. 初期状態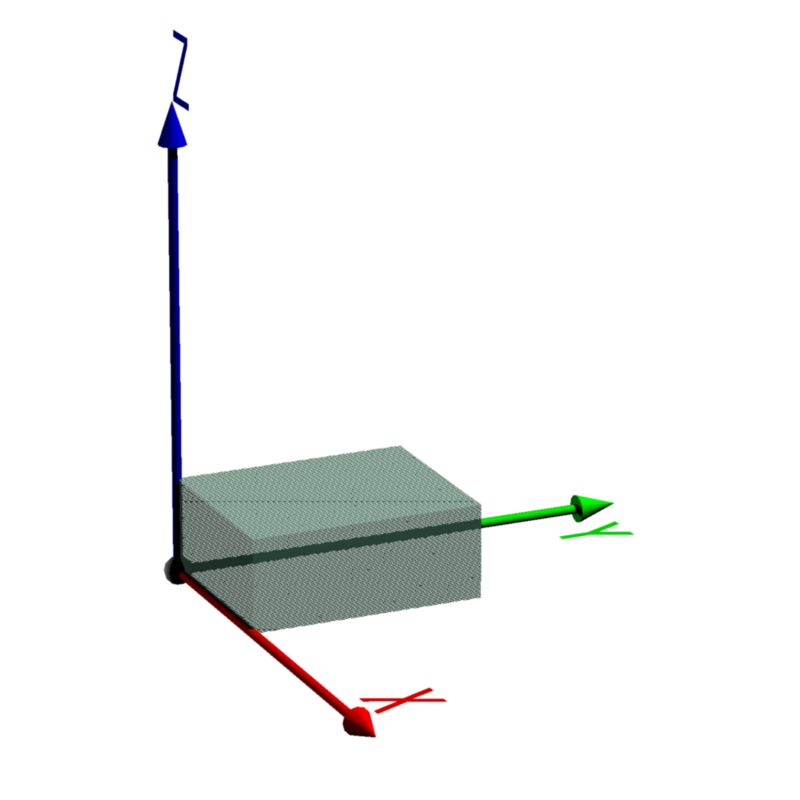
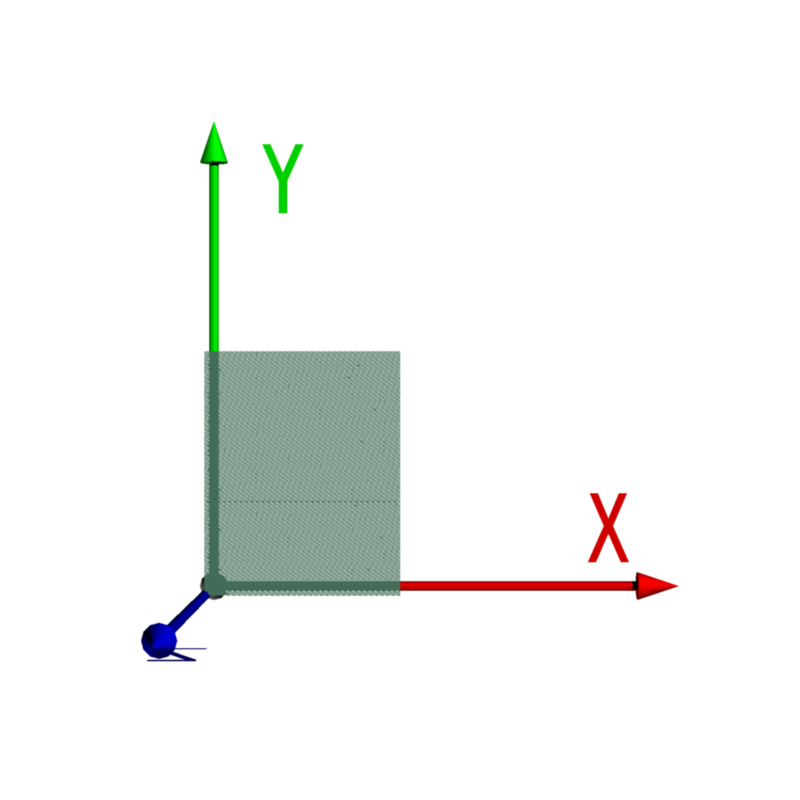1. X軸で回転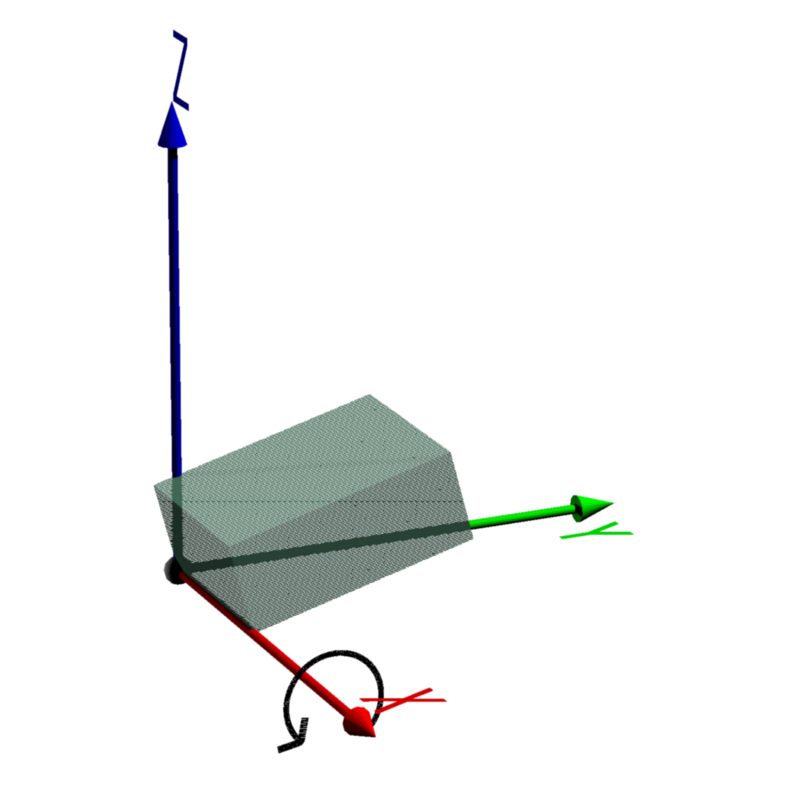
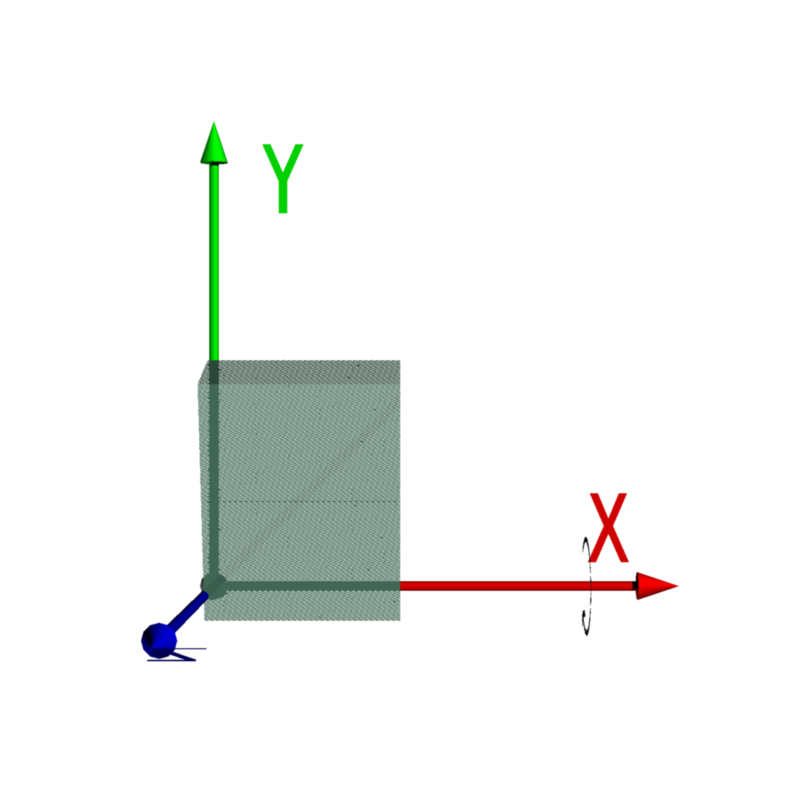2. Y軸で回転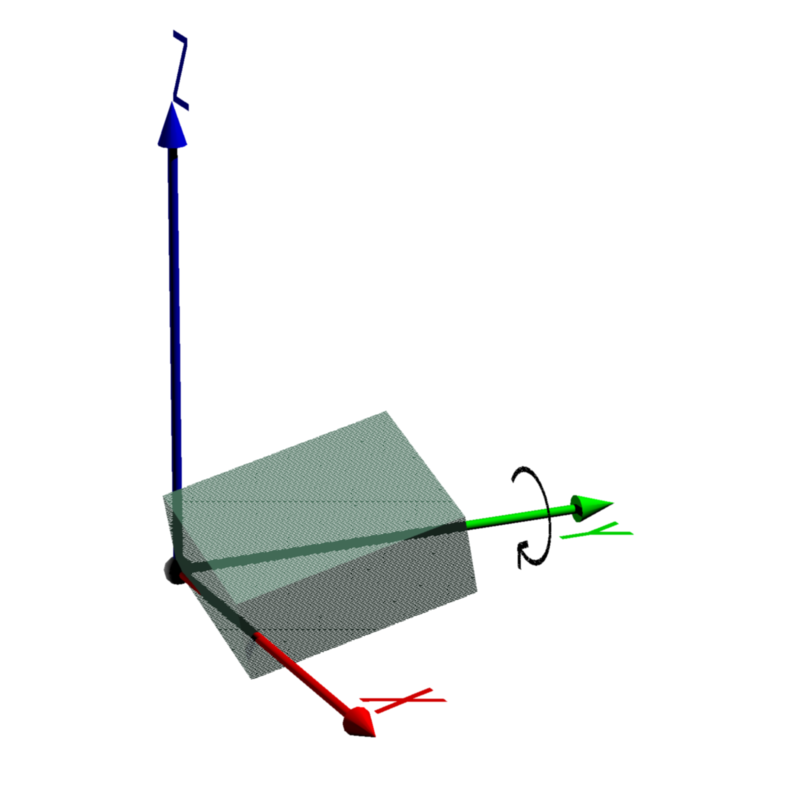
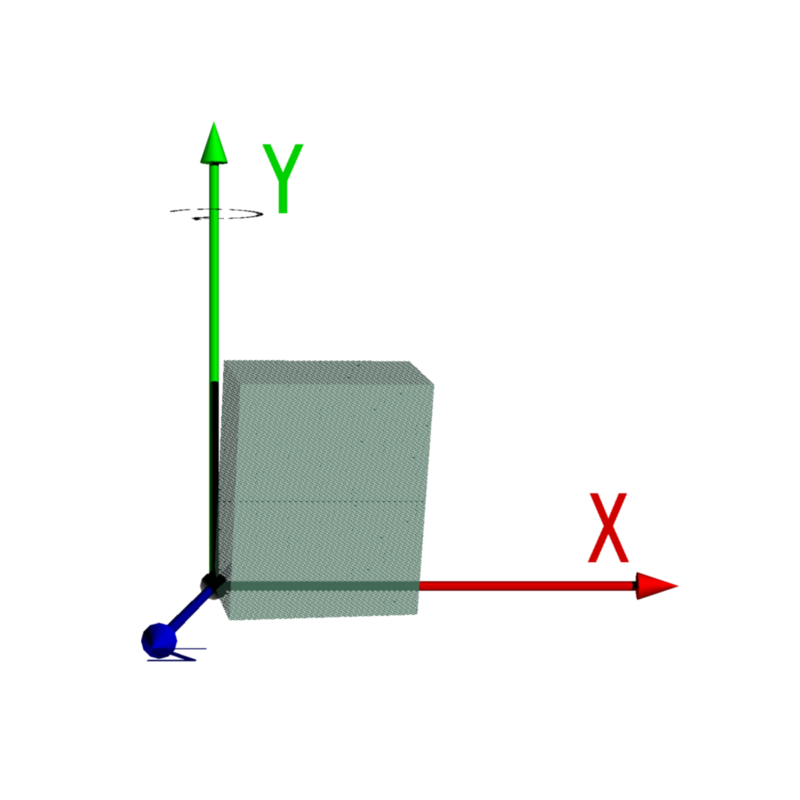3. Z軸で回転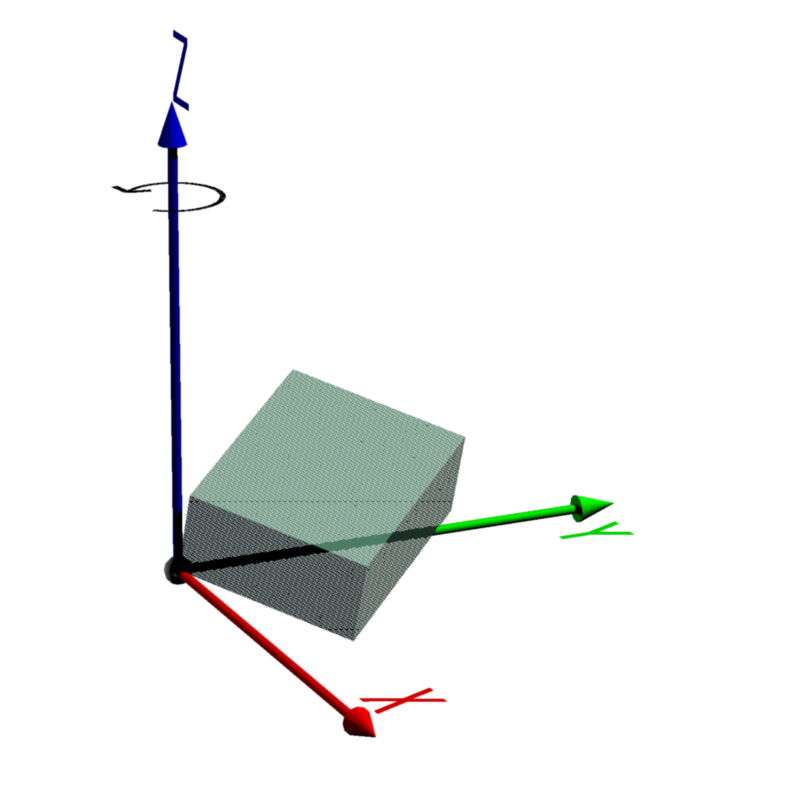

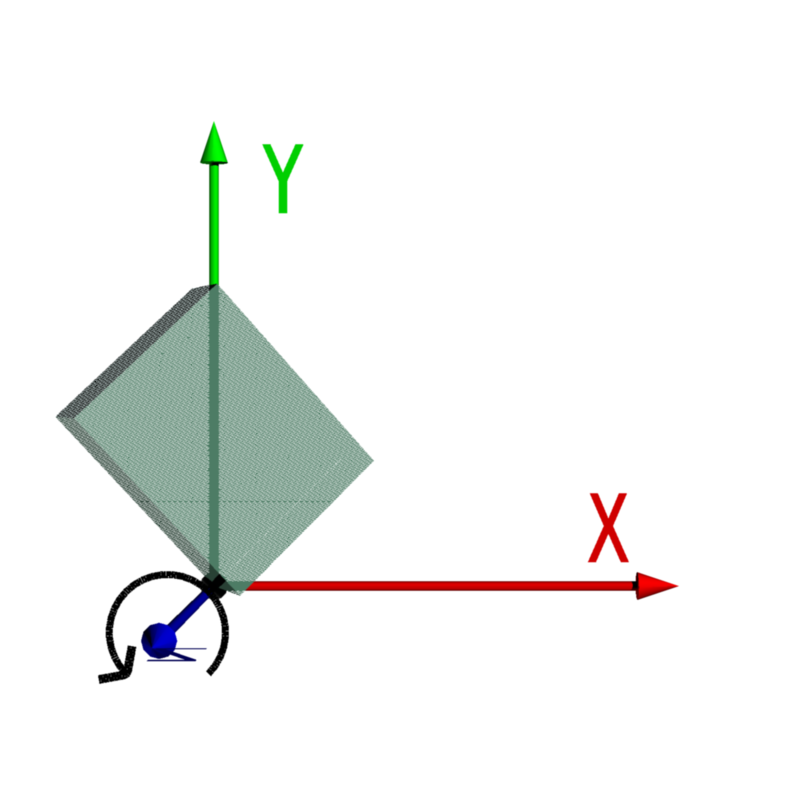以上これらを元に、例えば拡大 S を行い Z 軸で回転 Rz し、そして平行移動 T を行う変換は以下のように書けます。適用する順番と S、Rz、T の順番に注意してください。

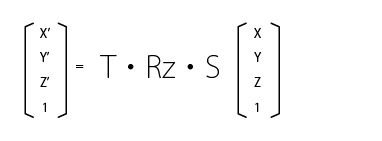
行列の積は結合法則が成り立つため、何段階かの変換を任意に一つの変換マトリックスに統合することができます。

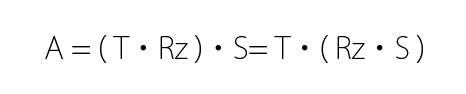
しかし、行列の計算は交換法則が一般に成り立たないため、この T Rz S の順は変更すると異なる変換となります。行列の計算は順番が大事です。

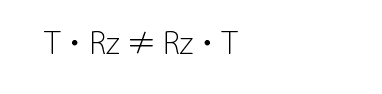
一般に変換順序は、スケール→回転（X→Y→Z）→平行移動という順で行われます。回転は X、Y、Z の各軸で三段階に分けて行いますが、目的によって異なる順や一部の軸の回転だけを採用する場合もあります。採用している順番を間違えないことが肝心です。

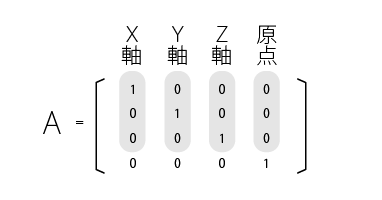
こうやって導き出したある座標を別の座標へ変換する変換マトリックスを A とすると、この変換マトリックスが　WCS　を基準としたある座標系を表していると解釈することができます。実際、変換マトリックスの各列は次の意味を持ちます。下は単位行列の変換マトリックスの場合です。

変換マトリックス A の逆行列 A-1 は、変換を元に戻す変換マトリックスになります。逆行列の定義から以下のように書けます。

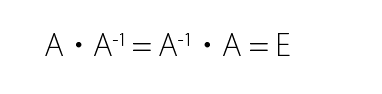
以下の関係をしっかり頭にいれてください。

• 変換マトリックス A は、それで表されるある座標系 A 上の座標を WCS の座標へ変換します。
• 逆行列 A-1 は WCS の座標を、変換マトリックス A で表されるある座標系 A 上の座標に変換します。